Формула Пика. Вычисление площади многоугольника изображенного на клетчатой бумаге.

Оказывается, площади многоугольников, вершины которых  расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика:                S = В + Г/2 - 1            Задача 1. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.).  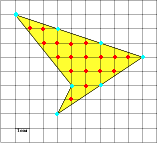Решение:  Целочисленные точки внутри многоугольника В = 18. Целочисленные точки на границе многоугольника Г = 7.  Применяем формулу: 18 + 7:2 – 1 = 20,5. Задача 2. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). 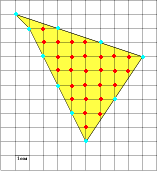Решение:  Целочисленные точки внутри многоугольника В = 27. Целочисленные точки на границе многоугольника Г = 10.  Применяем формулу: 27 + 10:2 – 1 = 31. Задача 3. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). 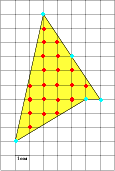Решение: Целочисленные точки внутри многоугольника В = 21. Целочисленные точки на границе многоугольника Г = 5. Применяем формулу: 21 + 5:2 – 1 = 22,5. Задача 4. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.).  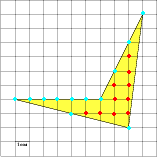Решение: Целочисленные точки внутри многоугольника В = 10. Целочисленные точки на границе многоугольника Г = 12. Применяем формулу: 10 + 12:2 – 1 = 15.  Задача 5. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). 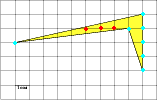Решение: Целочисленные точки внутри многоугольника В = 3. Целочисленные точки на границе многоугольника Г = 7. Применяем формулу: 3 + 7:2 – 1 = 5,5.